Factorial Digit Sum

Estava fazendo uma prova para um estagio como programador/desenvolvedor e aparece esta questão:

Create an algorithm, on your preferred language, that calculates the factorial digit sum. The factorial is represented by the ‘!’ operator. The ‘n’ represents a generic number. The ‘n!’ means n × (n − 1) × … × 3 × 2 × 1 For example, 10! = 10 × 9 × … × 3 × 2 × 1 = 3628800, and the sum of the digits in the number 10! is 3 + 6 + 2 + 8 + 8 + 0 + 0 = 27.

Find the factorial in the number 100!

Para explicar a questão, você tem que calcular o fatorial de um numero e logo pegar o resultado e somar cada digito dela. E eles pedem você calcular para o numero 100!, a resposta ta no final caso você queira resolver você mesmo. Em teoria isso é bem fácil de resolver, más como tudo na vida, nada é fácil em pratica.

Agora, eu tinha feito a minha solução ou melhor dito algoritmo no papel. Algoritmo, porque não cheguei a testar o maldito código. Lembrando que todo algoritmo que funciona pra nós, não necessariamente pode funcionar para o computador, em breve explicarei porque.

Esta foi a minha solução para esta questão feito em c#:

class Program
{
    static void Main()
    {
        ulong i,n,fatorial = 1,result = 0;

        n = 100;

        for(i = 1; i <= n ; i++){
            fatorial *= i;
        }

        Console.WriteLine(fatorial);

        do{
            result += fatorial % 10;
            fatorial = fatorial / 10;
        }while(fatorial > 0);

         Console.WriteLine(result);
    }
}

Agora si você já é um mestre em programação, você vai falar que isso não vai funcionar, e você ta certo. Por que não funciona? A variável ulong (que tem um tamanho de 64 bits ou 8 bytes) não tem o tamanho suficiente para armazenar o fatorial de 100. E qual é o fatorial de 100? 93326215443944152681699238856266700490715968264381621468592963895217599993229915608941463976156518286253697920827223758251185210916864000000000000000000000000

É, não é um numero pequeno. Da pra ver porque não caberia em uma variável de 8 bytes, nem na tela do meu site.

E com as maravilhas do .Net, fiz uma solução bem simples.

using System;
using System.Numerics;
namespace FactorialDigitSum
{
    class Program
    {
        static void Main(string[] args)
        {
            BigInteger factorial = new BigInteger(1);
            BigInteger result = new BigInteger(0);

            int n = 100;
            for (int i = 1; i <= n; i++)
                factorial *= i;

            do
            {
                result += factorial % 10;
                factorial /= 10;
            } while (factorial > 0);

            Console.WriteLine("Factorial Digit Sum of " + n + ": " + result.ToString());
        }
    }
}

Resultado da soma dos dígitos do fatorial de 100! = 648.

Yay, que fácil! É só usar a classe BigInteger que trabalha com números absurdamente grandes, que vai para facilitar a sua vida. E se a prova não quer o uso de qualquer classe e somente o uso de variáveis primitivas? Ai é problema seu, aqui só trabalho com .Net.

Não! Como cientista da computação, devo trazer todas as soluções. Porem viz a versão usando uma lista para armazenar cada digito do resultado fatorial. Assim podendo ser possível calcular números bem maiores.

A idea do método Multiply(int x, List bigNum) é calcular grandes números usando uma lista. Ilustrei o método usado para multiplicar na seguinte imagem:

using System;
using System.Collections.Generic;
using System.Numerics;

namespace FactorialDigitSum
{
    class Program
    {
        static void Main(string[] args)
        {
            int n = 100;
            Console.WriteLine("Factorial Digit Sum of " + n + ": " + CalculateFactorialDigitSum(n));
        }
        //Metodo usado para multiplicar grandes numeros usando uma lista
        public static void Multiply(int x, List<int> bigNum)
        {
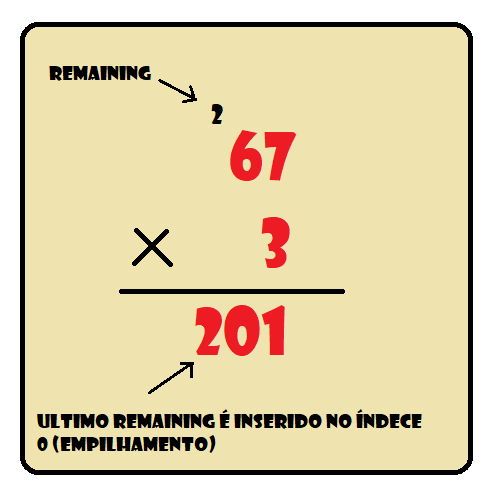
            int remaining = 0, sol;

            //Realiza uma multiplicão simples e guarda o sobrante da multiplicacão no remaining
            for (int i = bigNum.Count - 1; i >= 0; i--)
            {
                sol = remaining + bigNum[i] * x;
                bigNum[i] = sol % 10;
                remaining = sol / 10;
            }

            //Caso existir sobrante da multiplicação e si o numero tiver o digito maior do que 1 ele vai colocar cada digito em uma posição da lista
            while (remaining != 0)
            {
                bigNum.Insert(0, remaining % 10);
                remaining /= 10;
            }

        }
        //Metodo usado para calcular o fatorial de numeros grandes
        public static List<int> Factorial(int n)
        {
            List<int> result = new List<int> { 1 };
            if (n == 0)
                return result;

            //Multiplicação dos valores fatoriais
            // 10! = 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1
            // Cada digito vai ser guardado em uma posição da lista.
            for (int i = 1; i <= n; i++)
                Multiply(i, result);
            return result;
        }

        //Metodo usado para calcular a soma dos digitos do fatorial de um numero
        public static int CalculateFactorialDigitSum(int n)
        {
            List<int> factorial = Factorial(n);
            int result = 0;
            //Soma cada digito do resultado do fatorial
            for (int i = 0; i < factorial.Count; i++)
                result += factorial[i];
            return result;
        }

    }
}